SVR算法
概述
支持向量机(support vector machine)是一种分类算法,但是也可以做回归,也就是SVR。
-
SVM分类:找到一个分类平面,让两个分类集合的支持向量或者所以数据离分类平面最远。
-
SVR回归:找到一个回归平面,让一个集合的所以支持向量或者数据离回归平面的距离最近。
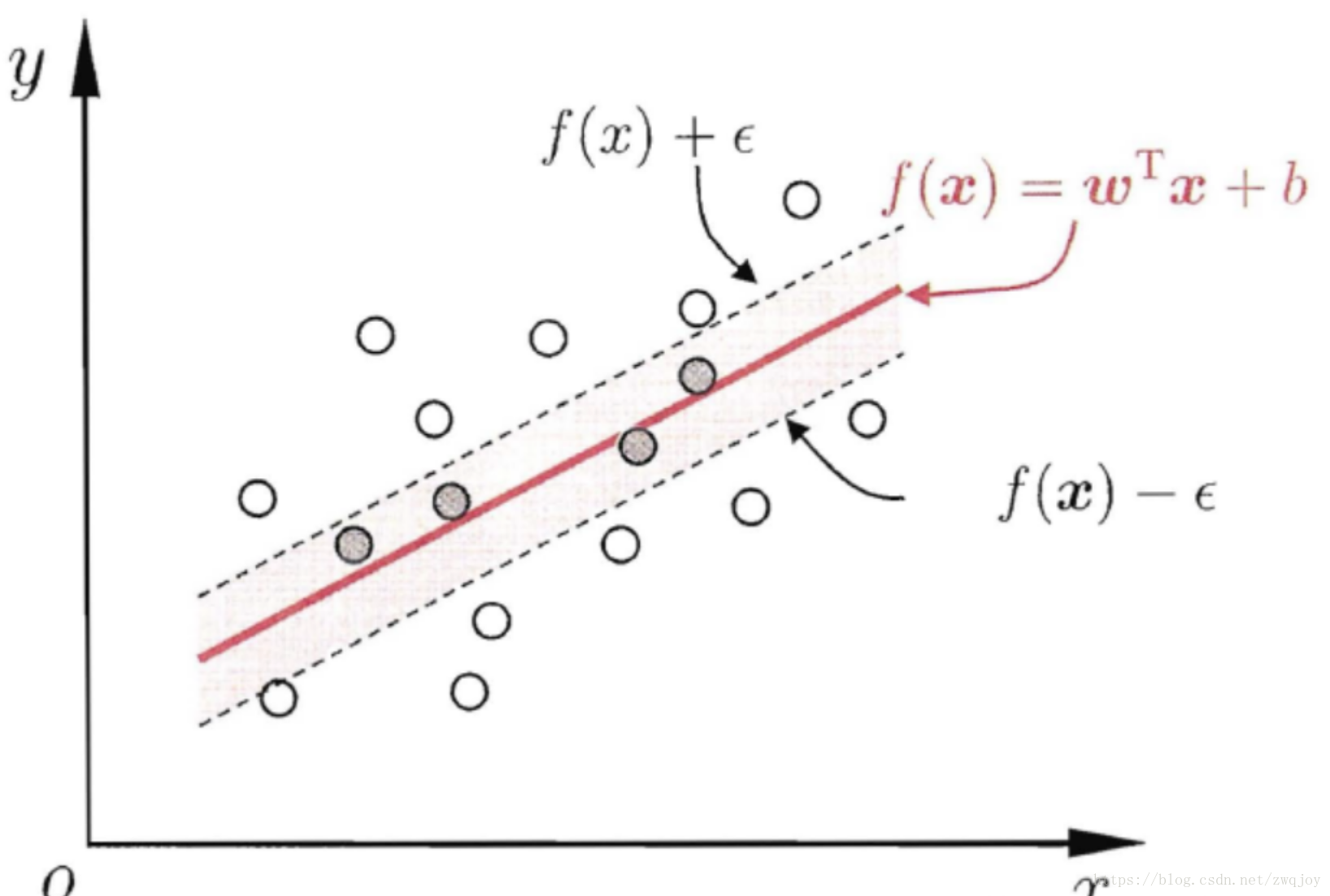
| 即SVR的思想就是:只要预测值与真实值的差距在一定范围内就认为预测是正确的,即设置阈值a,只要计算$ | f(x)-y | >a$ 的损失即可。对于非线性数据则需要采用SVM中核函数把数据投影到高维空间变成线性可分数据。具体算法有兴趣可自行了解. |
自己实现的例子——预测未来白菜价格
主要工作:利用SVR模型训练出一个预测白菜价格(利用每周历史数据预测下一天价格)的模型,数据集是2008年到2018年白菜的历史价格;数据集划分比例:7成训练,3成验证模型精确度。
- 准备好数据集,划分为训练集和测试集。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
from sklearn.svm import SVR
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
def load_data(filepath=r"data.csv", isTraining=True, days=7):
data = np.array(pd.read_csv(filepath,encoding="utf-8"))[:,1]
if isTraining:
data = data[:int(data.shape[0]*0.7)]
else:
data = data[int(data.shape[0]*0.7):]
x_data, y_data = [], []
for index in range(data.shape[0]-days):
x_data.append(data[index:(index+days)])
y_data.append(data[index+days])
x_data = np.array(x_data).astype(float)
y_data = np.array(y_data).astype(float)
return x_data, y_data
- 加载SVR模块,选择核函数kernel,惩罚因子C,核系数gamma.
- 常用的kernel函数: 高斯函数‘rbf’, 多项式函数‘poly’, 线性函数‘linear’.
- 惩罚因子C:表征你对离群点的重视,C越大越重视离群点,越不想丢掉他们。C值越大对误差惩罚增大,反之减少,当C趋于0时表示不再关注分类正确。一般使用大小为1e3.
- 核系数gamma: 是核函数‘rbg’,‘poly’,‘linear’的核系数且必须大于0. 随着核系数变化,存在模型过拟合情况。故需要调参。
1
2
3
4
def train(x_data, y_data):
clf = SVR(kernel='linear', C=1.0, epsilon=0.2)
model = clf.fit(x_data, y_data)
return model
- 使用训练好的SVR模型,预测未来值.
1
2
def test(x_data, model):
return model.predict(x_data)
- 使用matplotlib画出预测值和真实值的图像.
1
2
3
4
5
def plot_graph(y_test, y_pred):
plt.plot(y_pred, color='r', label=r"y_pred")
plt.plot(y_test, color='c', label=r"y_true")
plt.legend(loc='upper left')
plt.show()
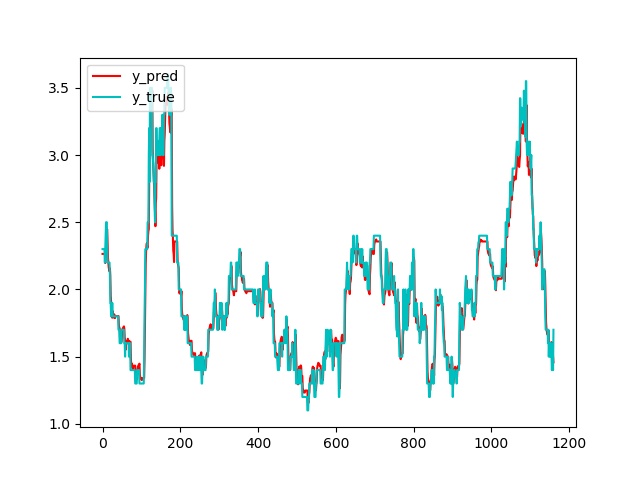
- 计算预测值和真实值之间的损失。使用了三种误差计算方式,分别为均方根误差,平均绝对值误差和 平均绝对百分比误差 .
1
2
3
4
5
6
7
8
9
def losses(y_pred, y_true):
RMSE = np.sqrt(np.mean((y_true-y_pred)**2))
MAE = np.mean(np.abs(y_true-y_pred))
MAPE = np.mean(np.abs(y_pred-y_true)/y_true)*100
print(
"RMSE:{}\n".format(RMSE),
"MAE:{}\n".format(MAE),
"MAPE:{}".format(MAPE)
)