回归模型

GBRT

提督提升回归树

Posted by hjw on November 16, 2019

GBRT

监督学习

给定样本 , 其中 的特征向量为 。 为第i个样本的标签，样本标签可以为离散值，如分类问题；也可以为连续值，如回归问题。监督学习就行，利用训练样本训练出模型，使得该模型能实现从样本到标签的映射：
为了计算出映射F(x),通常设置模型的损失函数L(y,F(x)),并求出损失函数最小情况下的映射为最好的映射 . 对于具体问题，我们一般构建训练样本到标签的映射关系，常见有线性模型和非线性模型。然后把问题转为求解映射函数中的参数问题。如线性模型: 求解模型即求解出最优参数W.

梯度下降法

梯度下降法（Gradient Descent）算法是机器学习中最常见算法，也是求解最优解最简单的方法，是一种迭代算法。对于优化问题minf(x) 其基本步骤为：

  • 随机选取一个初始点
  • 重复一下过程直到满足条件

    • 选择下降方向:

    • 选择步长img.

    • 更新点位置.

gd

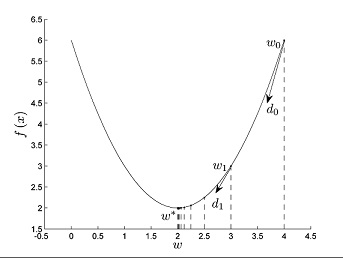
设置最终可以的到x的最优解

缺点：存在一下一种情况，当原函数有多个极小值点时，梯度下降只能找到一个极小值点，即可能只能找到函数的局部最优解，便“陷入”局部最优解里面出不来了。针对这种问题有很多改进算法，如批梯度下降法（batch gradient Descent）,动量随机梯度下降法（Momentum Stochastic Gradient Descent）等等，有兴趣可自行百度了解。

在函数空间优化

根据梯度下降的思路，对于模型的损失函数为L(y,F(x)),为了能求出最优函数F(x)，设置初始值, 把函数F(x)看成一个整体，对于每一个x,都存在对应函数值.与梯度更新法一直，经过m轮迭代可得最优函数

其中.

又因为F(x)由参数决定，由函数求导的链式法则可得

所以.

集成学习方法：Boosting方法

思想：对于一份数据，建立m个模型（弱分类器），每次分类都将上一次分错数据的权重修改再分类，再把所有分类器类加得到最终的分类器。

img

img

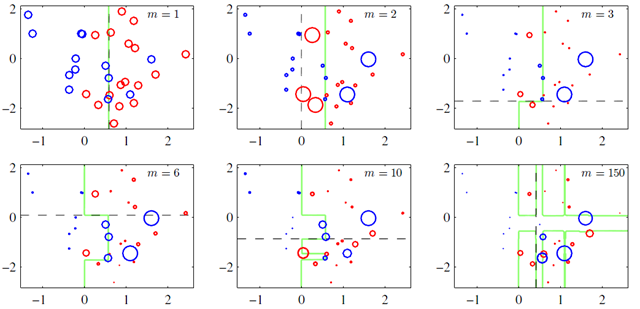
Gradient Boosting

由于在boosting方法中，最终预测结果为b个分类器结果的累加

梯度学习中最优函数为

可以直到boosting方法是一个求解梯度的方法，因此也成为基于梯度的Boost方法。

Gradient Boosting Regression Tree

梯度提升回归树是Gradient Boost框架下使用最多的算法，其学习器是分类回归树。

Classification And Regression Tree

分类回归树一棵满二叉树，即每个非叶子节点都有两个孩子。

对于样本。

算法大致流程：

  • 开始时把n个特征向量分配到根节点
  • 选取节点,把所有的向量划分到左孩子，的向量划分到右孩子。划分一种思路为:划分子树的方差最小。划分最优方法可以有很多。
  • 递归以上过程直至算法结束。

img

想了解具体过程可以自行百度。

梯度提升回归树

输入：，损失函数L(y,f(x)).

输出：回归树g(x)

算法流程:

  • 初始化,估计使损失函数最小的常数

  • 对

    • 对, 计算损失函数在当前模型的值，作为残差

    • 对拟合一个回归树，得到第m个树的叶节点区域为.

    • 对,计算损失函数最小化下的，叶节点区域的值。

  • 更新

  • 得到回归树

优点：

  • 可以灵活处理各种类型数据，包括连续值和离散值
  • 在相对较少的调参时间内，预测值比较准确。相对SVM而言
  • 在使用一些健壮的损失函数时，其鲁棒性较好

缺点：

  • 由于弱学习器之间存在较强的依赖关系，故较难训练。

训练GBRT模型预测白菜价格

  1. 准备数据集并按照比例划分
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

from sklearn.ensemble import GradientBoostingRegressor
import numpy as np 
import pandas as pd
import matplotlib.pyplot as plt

def load_data(filepath=r"data.csv", isTraining=True, days=7):
    data = np.array(pd.read_csv(filepath,encoding="utf-8"))[:,1]
    if isTraining:
    data = data[:int(data.shape[0]*0.7)]
    else:
    data = data[int(data.shape[0]*0.7):]
    x_data, y_data = [], []
    for index in range(data.shape[0]-days):
    x_data.append(data[index:(index+days)])
    y_data.append(data[index+days])
    x_data = np.array(x_data).astype(float)
    y_data = np.array(y_data).astype(float)
    return x_data, y_data

  1. 加载模型并调节参数

    在scikit-learning中，GradientBoostingClassifier对应GBDT的分类算法，GradientBoostingRegressor对应GBDT的回归算法。

    具体算法参数情况如下：

1

   GradientBoostingRegressor(loss=’ls’, learning_rate=0.1, n_estimators=100,  subsample=1.0, criterion=’friedman_mse’, min_samples_split=2,min_samples_leaf=1, min_weight_fraction_leaf=0.0, max_depth=3, min_impurity_decrease=0.0, min_impurity_split=None, init=None, random_state=None, max_features=None, alpha=0.9, verbose=0, max_leaf_nodes=None, warm_start=False, presort=’auto’, validation_fraction=0.1, n_iter_no_change=None, tol=0.0001)

参数说明：

  • n_estimators：弱学习器的最大迭代次数，也就是最大弱学习器的个数。
  • learning_rate：步长，即每个学习器的权重缩减系数a，属于GBDT正则化方化手段之一。
  • subsample：子采样，取值(0,1]。决定是否对原始数据集进行采样以及采样的比例，也是GBDT正则化手段之一。
  • init：我们初始化的时候的弱学习器。若不设置，则使用默认的。
  • loss：损失函数，可选{‘ls’-平方损失函数，’lad’绝对损失函数-,’huber’-huber损失函数,’quantile’-分位数损失函数}，默认’ls’。
  • alpha：当我们在使用Huber损失”Huber”和分位数损失”quantile”时，需要指定相应的值。默认是0.9，若噪声点比较多，可适当降低这个分位数值。
  • criterion：决策树节搜索最优分割点的准则，默认是”friedman_mse”，可选”mse”-均方误差与’mae”-绝对误差。
  • max_features：划分时考虑的最大特征数，就是特征抽样的意思，默认考虑全部特征。
  • max_depth：树的最大深度。
  • min_samples_split：内部节点再划分所需最小样本数。
  • min_samples_leaf：叶子节点最少样本数。
  • max_leaf_nodes：最大叶子节点数。
  • min_impurity_split：节点划分最小不纯度。
  • presort：是否预先对数据进行排序以加快最优分割点搜索的速度。默认是预先排序，若是稀疏数据，则不会预先排序，另外，稀疏数据不能设置为True。
  • validationfraction：为提前停止而预留的验证数据比例。当n_iter_no_change设置时才能用。
  • n_iter_no_change：当验证分数没有提高时，用于决定是否使用早期停止来终止训练。
1
2
3
4
5
6
7

def train(x_data, y_data):
    model = GradientBoostingRegressor(
      n_estimators=100,
      learning_rate=0.1,
      loss='ls'
    )
    return  model.fit(x_data, y_data)
  1. 测试数据集并计算出损失值
1
2
3
4
5
6
7
8
9
10
11
12

def test(x_test, model):
    return model.predict(x_test)
    
def losses(y_pred, y_true):
    RMSE = np.sqrt(np.mean((y_true-y_pred)**2))
    MAE = np.mean(np.abs(y_true-y_pred))
    MAPE = np.mean(np.abs(y_pred-y_true)/y_true)*100
    print(
      "RMSE:{}\n".format(RMSE),
      "MAE:{}\n".format(MAE),
      "MAPE:{}".format(MAPE)
    )
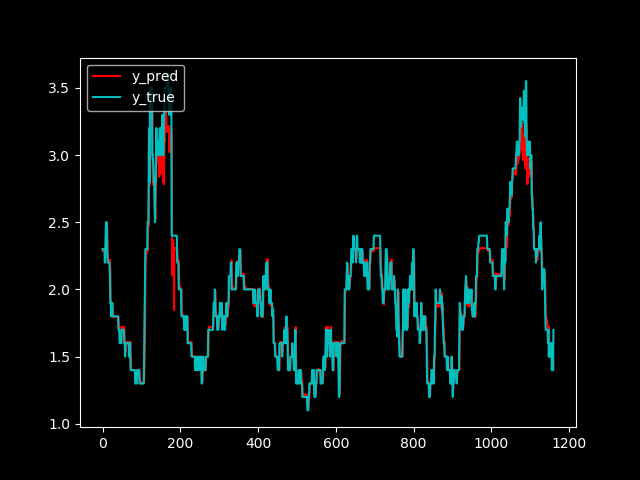
  1. 画出预测图跟真实数据图
1
2
3
4
5
6
7
8

def plot_graph(y_test, y_pred):
    plt.figure()
    plt.style.use('dark_background')
    plt.plot(y_pred, color='r', label=r"y_pred")
    plt.plot(y_test, color='c', label=r"y_true")
    plt.legend(loc='upper left')
    plt.show()

img

代码传送门

FEATURED TAGS
回归模型
FRIENDS